概念

向量

向量是有大小和方向的有向线段

A->B的向量，公式为B点-A点

向量没有位置，只有大小和方向

例：(1,4,6)、(4,3.7)、(0,0,0)

标量

只有大小，没有方向

例：5

点

有位置，没有大小和方向

例：(1,4,6)、(4,3.7)、(0,0,0)

零向量

零向量是没有大小和方向的向量

例：(0,0,0)

向量的模长

向量的模长指向量的长度 即向量的大小。向量a的模记作|a|

在线性代数中，向量的模通常用在向量两边各加两条竖线的方式表示，如||v||，表示向量v的模。向量的模的计算公式如下：

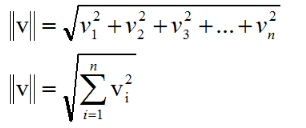
对于2D，3D向量的如下

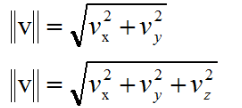
例：(-12,5)的模长为：

√(-12)² + 5² = √144 + 25 = √169 = 13

标准化向量（单位向量）

所谓的标准化向量就是单位向量，就是向量的长度为1的向量

适用于只关心方向，不关心大小的情况。比如法线

对于任意非零向量v，都能计算出一个和v方向相同的单位向量n，这个过程被称作为向量的“标准化”，要标准化向量，将向量除以它的大小（模）即可。

单位向量=向量/模长

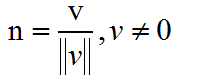
例：(-12,5)/13 = (-0.92,0.38)

公式

标量与向量的运算

可以乘除、不可以加减运算

标量与向量元素分别相乘/相除

例：-2(2,-5) = (-4,10)、(6,-2,-4) / 2 = (3,-1,-2)

向量与向量的加减法运算

前提，如果两个向量的维数相同，那么他们能够相加减，运算结果的向量的维数和原向量相同

公式

(a_x,a_y) + (b_x,b_y) = (a_x+ b_x,a_y + b_y)

(a_x,a_y) - (b_x,b_y) = (a_x - b_x,a_y - b_y)

例：(-1,4) + (3,-5) = (2,-1)

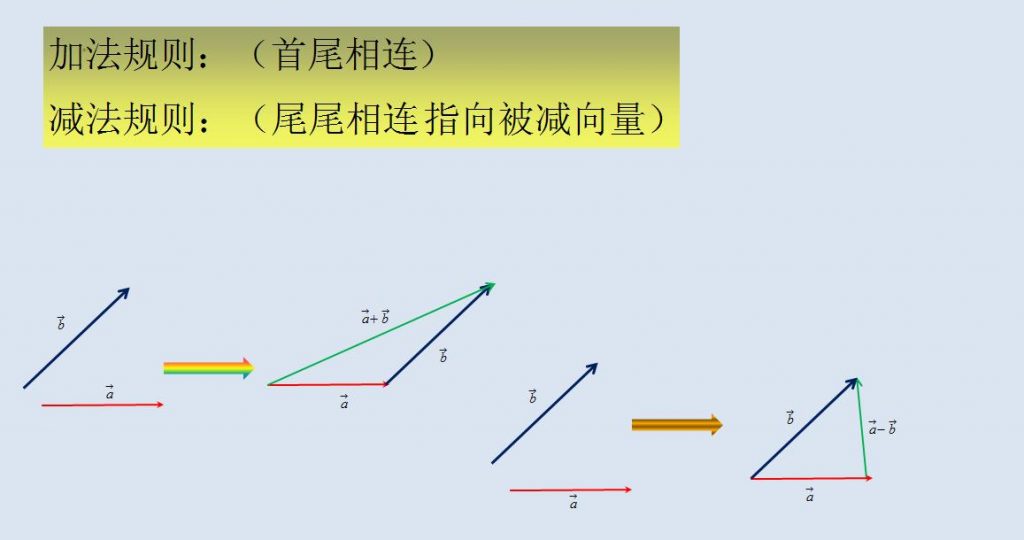
距离公式

距离公式的推导

通过上面的三角形原则，我们可以发现，通过两个向量的加减可以得到第三个向量，我们将这个过程逆置，如果知道了两点的距离，如何求出其距离，我们可以利用向量的减法实现。

运算公式

在3D中，已知两点a，b，求两点之间的距离d？我们可以将a，b两点看做向量，然后b-a就是向量d，然后我们再计算向量d的模就是两点间的距离

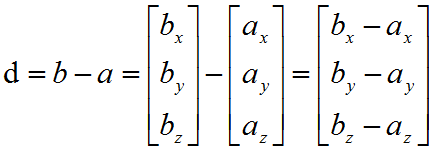
求出向量d后，再求d的模就是两点的距离

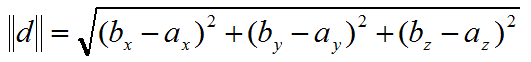
向量的点积（点乘、内积）

基本概念

标量可以和向量相乘，向量也可以和向量向量相乘，这就叫点乘，也叫做内积。标量与向量相乘不可以写点，向量与向量相乘必须要写点，向量的点乘优先级高于向量的加减法。注意：向量点乘后的结果是标量

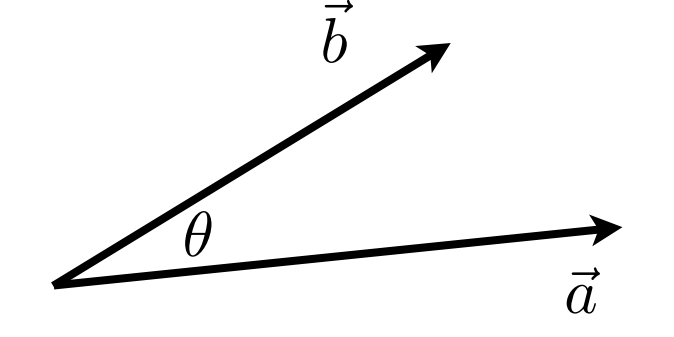
向量的点乘描述的是两个向量的相似程度，即两个向量之间的夹角的大小

运算公式

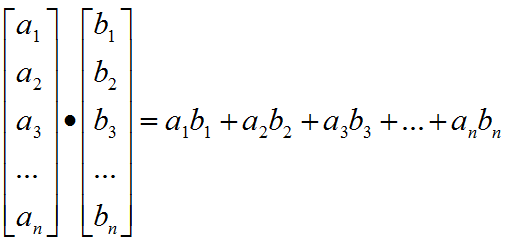
应用到2D，3D中为

a·b = a_xb_x + a_yb_y

a·b = a_xb_x + a_yb_y+ a_zb_z

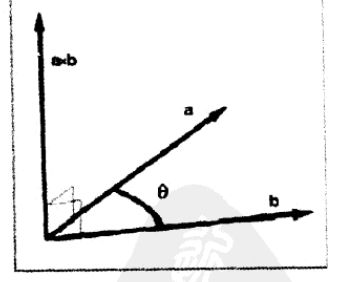
a向量点乘b向量 = a长度 * b长度 * cos夹角

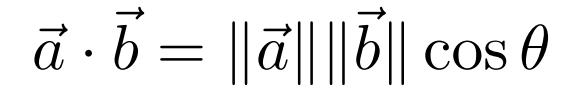
那么cos夹角 = (a向量 * b向量) / (a长度 * b长度)

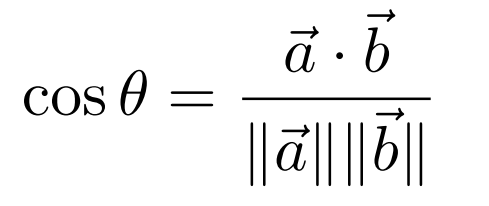
在2D中表示为：

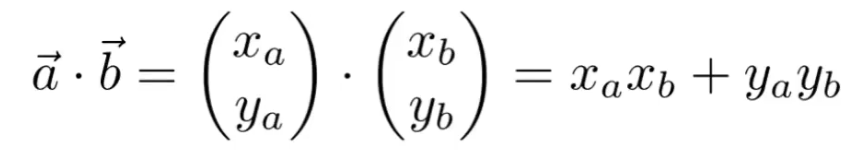
在3D中表示为：

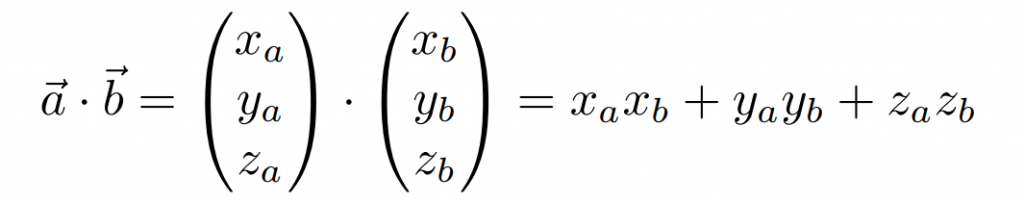
可以求出cos夹角 = a单位向量 * b单位向量

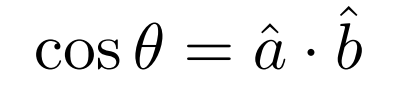
点乘满足以下公式

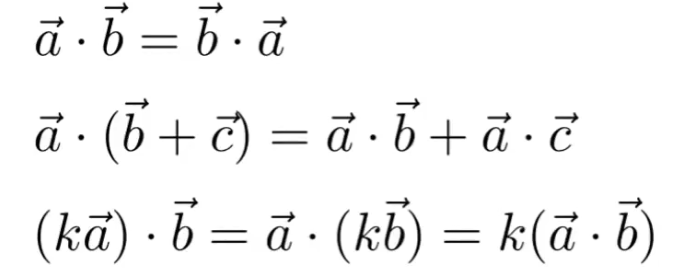
测出向量再前还是后

设立一个方向为正方向，若一向量与该方向的向量点乘 >0 则该向量指向所规定的正方向反之为反方向

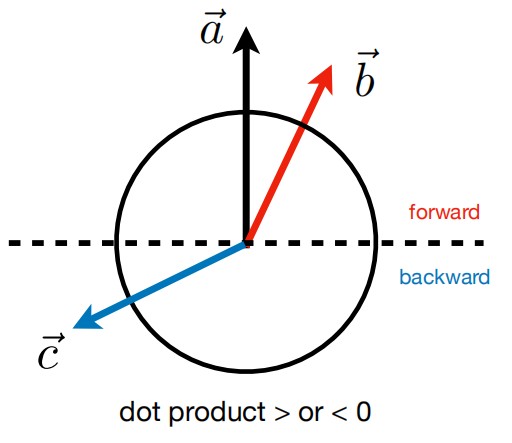
运算说明

a · b > 0    方向基本相同，夹角在0°到90°之间

a · b = 0    正交，相互垂直  

a · b < 0    方向基本相反，夹角在90°到180°之间 

向量的投影

基本概念

给定两个向量v和n，能将v分解成两个分量，一个是垂直于向量n，一个平行于向量n，平行于向量n的向量我们称为在向量n上的投影。

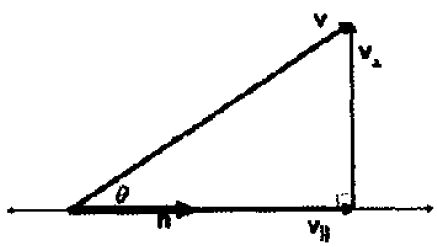
投影的求解

因为向量n平行于投影向量，所以可以求出向量n的单位向量再乘以投影的模，就可以得到投影向量，如下

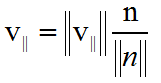
我们接下来求投影的模即可，我们可以根据三角函数的余弦公式来求出投影的模

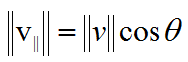
代入投影的模就可以求出投影向量

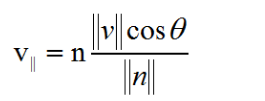
又因为

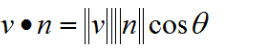
所以

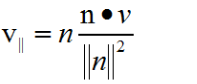
垂直向量的求解

根据三角形法则，可以轻易求出垂直的向量

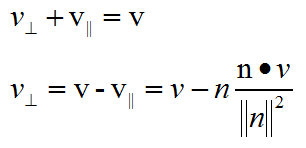
向量的叉积（叉乘）

基本概念

两个向量的叉乘得到是向量，且这个向量垂直于原来的两个向量。向量的叉乘只可以运用在3D向量中。

• 叉乘结果与两个初始向量正交，即垂直于两个初始向量形成的平面
• 由右手定则规定叉乘结果向量的方向（在一些类似OpenGL里可能是用的左手坐标系）
• 可用作构造坐标系

数学运算公式

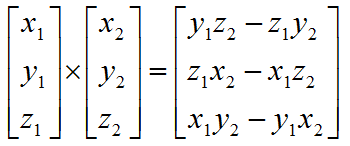
几何运算公式

向量叉乘的结果向量的长度与两个向量的夹角有关，且成正弦函数关系，如果向量a和b是平行关系，则叉乘的结果为0，因为sin0为0

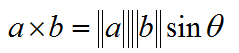
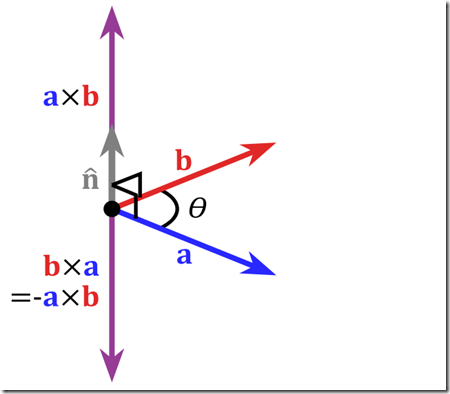
向量叉乘方向的判断

向量的叉乘是通过右手定则来判断结果向量的方向的。伸出右手，四指弯曲符合向量叉乘的顺序，那么大拇指就是叉乘后结果向量的方向。如下图axb，右手四指弯曲方向从a到b，大拇指方向向上就是叉乘结果向量的方向

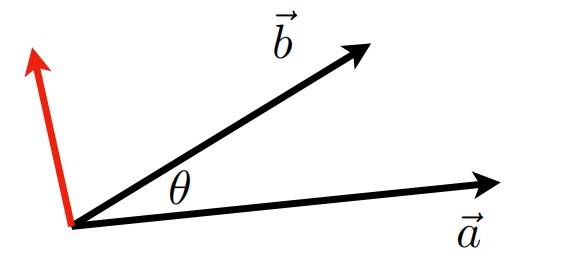
向量叉乘在图形学中的应用

判断向量在另一个向量的左边还是右边

由右手定则规定叉乘结果向量的方向 ，如 a x b，a在b的前面，右手除大拇指外其余四个手指并排同指向a向量方向，大拇指垂直于四指并排方向，四指延向量a与向量b的夹角 θ 旋转到向量b，大拇指做值方向为叉乘的方向，若是b x a，b在a的前面，那么结果的方向与a在b前面的的方向相反。因此可以借此判断一个向量是在另一个向量的左边还是右边。

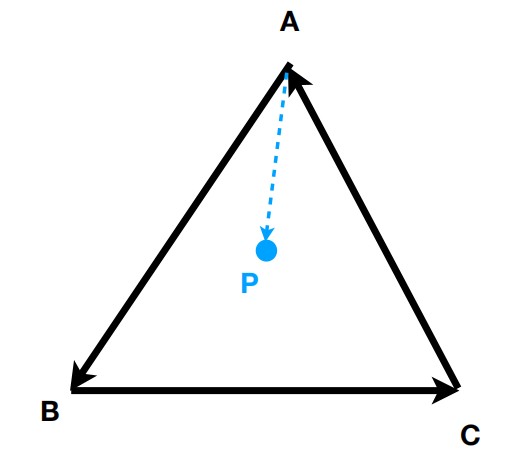
判断点在里面还是外面

如下图，计算 向量AB x 向量AP，向量BC x 向量BP，向量CA x 向量CP，由右手定则规定叉乘结果向量的方向这一特性可以判断向量在另一个向量的左边还是右边，所以经过上面的计算若3个结果是同号的话，那么在点P在三角形的里面，若三个结果中有一个结果与其他的结果符号不同那么P点在三角形外面。

最后编辑：2022-01-25

作者：网虫虫

分享是一种快乐； 分享是一种美德； 分享是一种幸福！

站内专栏 站点 QQ交谈