GAMES101-线性代数（矩阵）

概念

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 ^[1] ，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。

行矩阵、列矩阵

m×n阶矩阵中，m=1，称为行矩阵，也称为n维行向量;n=1，称为列矩阵，也称为m维列向量。

零矩阵

所有元素都为0的m×n阶矩阵

n阶方阵

m×n阶矩阵A中，m=n; n阶方阵A，可定义行列式记为|A|; n阶方阵存在主对角线及主对角线元素。

单位矩阵

主对角线上的元素都为1，其余元素均为0的n阶方阵称为n阶单位矩阵，记为E。

对角形矩阵

非主对角线上的元素全为0的n阶方阵称为对角形矩阵。

数量矩阵

n阶对角形矩阵主对角线上元素相等时，称为数量矩阵。

上（下）三角形矩阵

n阶方阵中，主对角线下方元素全为零，称为上三角矩阵;主对角线上方元素全为零，称为下三角矩阵。

同型矩阵

A=aij(m×n),B=bij(s×t),m=s、n=t,A与B为同型矩阵，若对应元素相等，则A与B相等。

转置矩阵

将矩阵A的行列互换，而不改变其先后次序得到的n×m阶矩阵，记为

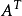
或A’。

对称矩阵与反对称矩阵

设A是n阶方阵，如果A^T=A,则称A是对称矩阵。如果

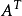
=-A,则称A为反对称矩阵。反对称矩阵中，主对角线上的元素均为0。

逆矩阵

设A是n阶方阵，若存在一个n阶方阵B，使得AB=BA=E,则B称为A的逆矩阵，A称为可逆矩阵或非奇异矩阵。（可逆矩阵一定是方阵，并且它的逆矩阵为同阶方阵；A与B地位是等同的，所以B也是可逆矩阵，并且A是B的逆矩阵。）记为A-1,AA-1=A-1A=E.

伴随矩阵

设矩阵A，Aij为行列式|A|中元素aij的代数余子式，称A*为矩阵A的伴随矩阵。AA*=A*A=|A|E

可逆矩阵

|A|≠0。(A可逆时，A-1=A*/|A|)

正交矩阵

设A为实数域R上的方阵，如果它满足A^TA=AA^T=E,则称A为正交矩阵。

准对角形矩阵

设A为n阶方阵，如果它的分块矩阵具有如下形式，

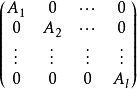
，则称A为准对角形矩阵。

矩阵的初等变换

互换、倍乘、倍加。矩阵的初等行变换和初等列变换统称为矩阵的初等变换。

阶梯形矩阵

若矩阵A满足两条件：（1）若有零行（元素全为0的行），则零行应在最下方；（2）非零首元（即非零行的第一个不为零的元素）的列标号随行标号的增加而严格递增，则称此矩阵A为阶梯形矩阵。

简化阶梯形矩阵

(1)零行(元全为零的行)位于全部非零行的下方(若有)；(2) 非零行的首非零元的列下标随其行下标的递增而严格递增。(3)非零行的首非零元为1；(4)非零行的首非零元所在列的其余元均为零。

初等矩阵

由单位矩阵E经过一次初等变换得到的矩阵称为初等矩阵。

公式

矩阵的加减法

1、运算规则

只有同型矩阵之间才可以进行加减法运算，将两个矩阵相同位置的元相加减即可，m行n列的两个矩阵相加减后得到一个新的m行n列矩阵，例如：

加法

减法

简言之，两个矩阵相加减，即它们相同位置的元素相加减！

注意：只有对于两个行数、列数分别相等的矩阵（即同型矩阵），加减法运算才有意义，即加减运算是可行的．

2、 运算性质 （假设运算都是可行的）

满足交换律和结合律

交换律：A+B = B+A

结合律：(A+B)+C = A+(B+C)

矩阵与数的乘法

1、运算规则

数乘即将矩阵乘以一个常量，矩阵中的每个元都与这个常量相乘，例如：

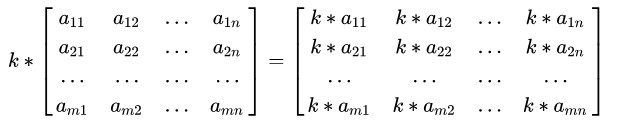
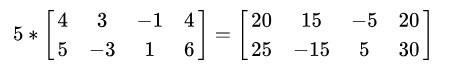
2、 运算性质

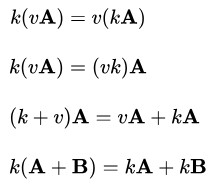
矩阵与矩阵的乘法

1、运算规则

两个矩阵的乘法仅当第一个矩阵的列数和另一个矩阵的行数相等时才能定义，m×n 矩阵 A 和 n×p 矩阵 B 相乘，会得到一个 m×p 矩阵 C，记为 C = AB。

C中第i行i列的元即为：

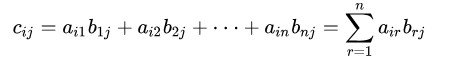
式子看着很复杂，其实很简单， C 中第i行第j列的元素的值为： A 中第i行所有元素 与 B 中第j列的所有元素一一对应相乘，然后将相乘后的所有值相加。

例如：

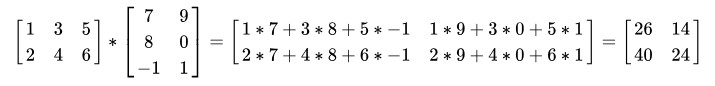
2、 运算性质

(AB)C = A(BC)

(A+B)C = AC+BC

C(A+B) = CA+CB

不满足交换律 即AB ≠ BA

例如1*3的矩阵乘以3*1的矩阵得到的是1*1的矩阵（每n行乘以每n列，左边只有一行，右边只有一列，向量的点乘就属于这种情况）：

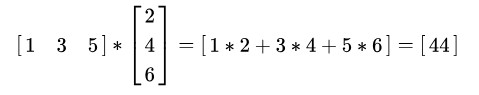
而把它们反过来，即3*1的矩阵乘以1*3的矩阵，就变成了3*3的矩阵：

矩阵与向量相乘

1、运算规则

向量用矩阵表示的话，是属于一个n*1的矩阵，例如

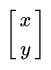二维向量： 三维向量：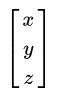

因此一个 m * 2 的矩阵可以乘以一个二维向量，m * 3 的矩阵可以乘以一个三维向量。

这点对于向量的变换运算非常的重要，例如我们想要将向量 (x, y) 做一个y轴的对称操作，即变为 (-x, y) ，只需要用下面的矩阵乘以这个向量即可：

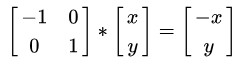
矩阵表示向量的点积

矩阵表示向量的叉积

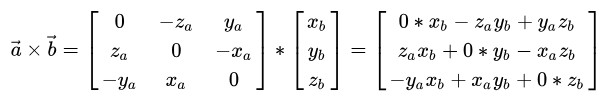
至于左边这个矩阵怎么来的？可以看后续的三维旋转推导。

矩阵转置

1、运算规则

把矩阵 A 的行和列互相交换所产生的矩阵称为A的转置矩阵（标记为 A^T ），这一过程称为矩阵的转置。

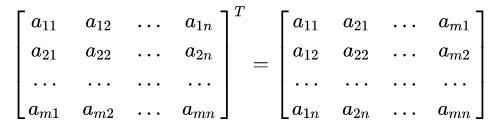
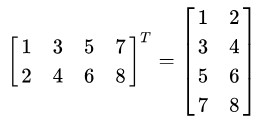
2、 运算性质

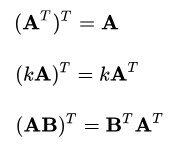
矩阵共轭

对于一个复数矩阵 A ，我们对其做实部不变，虚部取负的操作即为共轭操作，记作 。例如

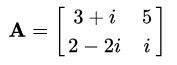
则

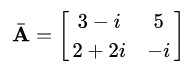
部分内容摘自：https://zhuanlan.zhihu.com/p/362082020

最后编辑：2022-01-25

作者：网虫虫

分享是一种快乐； 分享是一种美德； 分享是一种幸福！

站内专栏 站点 QQ交谈